排序算法（二）

2020-04-29

快速排序、基数排序、选择排序、希尔排序

快速排序

平均时间复杂度O(nlogn) 空间复杂度O(logn)~O(n) 最好情况O(nlogn) 最坏情况O(n²) 不稳定

图解

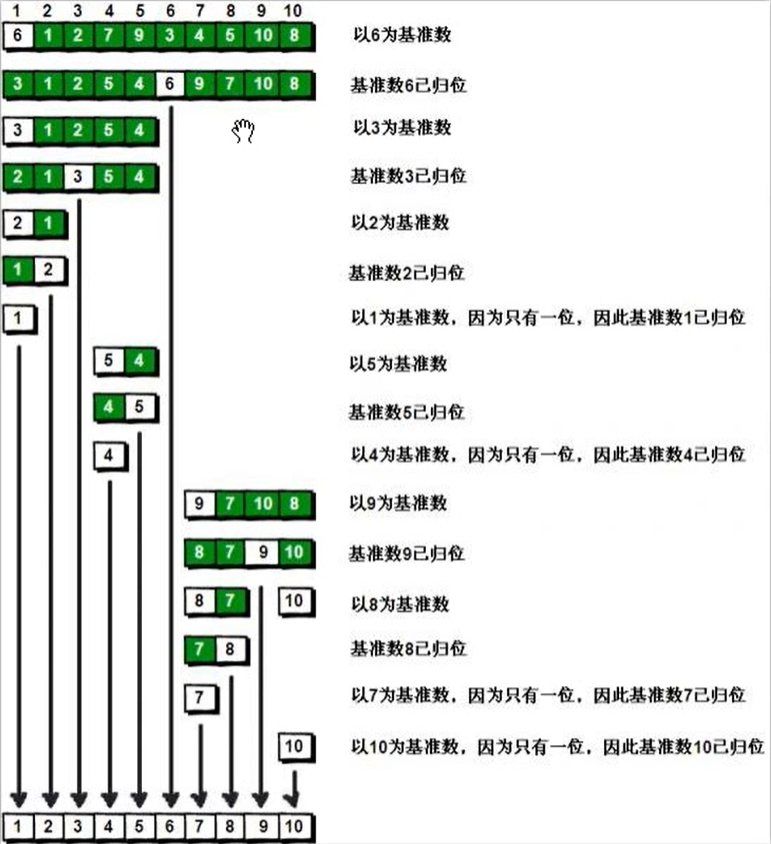
cenganhui/TOIMG3ea820607085911N.png

流程：

把数组中最左边的数当做基准，然后从两边进行检索。
先从右边往左边检索，检索到比基准小的，停下。
从左边往右边检索，检索到比基准大的，停下。
交换两个数，然后继续上面两步的检索。
当i=j相遇的时候，将基准所在元素和相遇位置元素进行交换。（确定下了基准数的最终位置，而且这个数左边的都比它小，右边的都比它大）
进入基准的左区间，重复上面的流程。
进入基准的右区间，重复上面的流程。

public static void quickSort(int[] arr,int left,int right){
    if(left > right){   //判断，若左索引>右索引，直接返回
        return ;
    }
    int i = left;   //左索引
    int j = right;  //右索引
    int base = arr[left];   //保存基准
    while(i != j){  //当i和j未相遇
        while(i<j && arr[j]>=base){ //i<j并且从右往左找比基准小的，找到就停下，否则j左移
            j--;
        }
        while(i<j && arr[i]<=base){ //i<j并且从左往右找比基准大的，找到就停下，否则i右移
            i++;
        }
        //找到这两个数后进行交换
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    //当循环不满足时，i和j相遇，交换基准所在元素和相遇位置元素
    arr[left] = arr[i];
    arr[i] = base;
    //这一轮排序完成了，左区间都比基准小，右区间都比基准大
    //递归进入左区间继续排序
    quickSort(arr,left,i-1);
    //递归进入右区间继续排序
    quickSort(arr,i+1,right);
}

基数排序

平均时间复杂度O(nk) 空间复杂度O(n+k) 最好情况O(nk) 最坏情况O(n*k) 稳定

流程：

找出数组中最大的数，确定这个最大数的位数n，进行n轮排序，每一轮是第i轮。（i=0，按个位排；i=1，按十位排…）
创建10个桶（二维数组），编号为0-9，分别对应位数中的0-9。
（如果是第一轮）将数组中的元素按照个位上的大小放入对应的桶（数组）中。
从0-9个桶（数组）中一次按照加入的先后顺序取出，放回原数组中。（这一轮便结束）
（进行第二轮）将数组中的元素按照十位上的大小放入对应的桶（数组）中。
同上流程，直到进行完n轮排序之后，原数组就是有序的数组了。

public static void radixSort(int[] arr){
    //找到数组中的最大数
    int max =arr[0];
    for(int i=0;i<arr.length;i++){
        if(max < arr[i]){
            max = arr[i];
        }
    }
    int maxLen = (max + "").length();   //与字符串相加获得最大数有几位
    int[][] bucket = new int[10][arr.length];   //创建10个桶
    int[][] bucketCount = new int[10];  //用一维数组记录10个桶中元素的个数
    //进行maxLen轮排序
    for(int i=0,n=1;i<maxLen;i++,n*=10){
        //遍历数组
        for(int j=0;j<arr.length;j++){
            int digit = arr[j] / n % 10;    //算出当前元素对应位的值
            bucket[digit][bucketCount[digit]] = arr[j]; //根据这个值放入对应的桶中
            bucketCount[digit]++;   //对应桶中元素个数+1
        }
        int index = 0;  //原数组索引
        for(int k=0;k<bucket.length;k++){   //遍历10个桶
            if(bucketCount[k] != 0){    //当桶中有元素时
                for(int l=0;l<bucketCount[k];l++){  //遍历这个桶
                    arr[index] = bucket[k][l];  //将桶中元素放回到原数组
                    index++;    //原数组索引后移
                }
            }
            bucketCount[k] = 0; //将这个桶中元素个数归0
        }
    }
}

选择排序

平均时间复杂度O(n²) 空间复杂度O(1) 最好情况O(n²) 最坏情况O(n²) 不稳定

流程：

进行n-1轮排序。
每一轮排序，又是一个循环遍历。
1. 假设当前数是最小数。
2. 用最小数和后面的每个数进行比较，如果发现有比最小数更小的数，则重新确定最小数，并记录下最小数的下标。
3. 遍历到最后时，就得到本轮的最小数和下标。
4. 交换当前数和最小数

public static void selectSort(int[] arr){
    //进行n-1轮排序
    for(int i=0;i<arr.length-1;i++){
        int min = arr[i];   //假设第一个是最小数
        int minIndex = i;   //记录下标
        for(int j=i+1;j<arr.length;j++){    //向后遍历
            if(arr[j] < min){   //如果比最小数更小，则重新确定最小数并记录下标
                min = arr[j];
                minIndex = j;
            }
        }
        if(minIndex != i){  //如果最小数更新了，就交换当前数和最小数
            arr[minIndex] = arr[i];
            arr[i] = min;
        }
    }
}

希尔排序

平均时间复杂度O(n1.3) 空间复杂度O(1) 最好情况O(n) 最坏情况O(n²) 不稳定

流程：

设置步长，一般设置为length/2，然后每一轮步长/2。
每一轮按步长进行分组。
每组内使用插入排序。
当步长缩小到1时，便进行最后一次排序，结束后数组就有序了。

public static void shellSort(int[] arr){
    //设置步长gap=length/2，每一轮步长/2
    for(int gap=arr.length/2;gap>0;gap/=2){
        //每一次设置步长分组后，组内进行插入排序
        int insertVal = 0;
        int insertIndex = 0;
        for(int i=gap;i<arr.length;i++){
            insertVal = arr[i]; //无序区中第一个
            insertIndex = i - gap;  //无序区的前一个，即有序区的最后一个
            //当不越界，且<（即还未找到插入位置）时
            while(insertIndex>=0 && insertVal<arr[insertIndex]){
                //按步长将元素后移（即组内元素后移）
                arr[insertIndex + gap] = arr[insertIndex];
                insertIndex -= gap;
            }
            //循环结束后就找到插入位置并执行插入
            arr[insertIndex + gap] = insertVal;
        }
    }
}